【WebGL】GLSLで使う数学(三角関数、ベクトル)を文系エンジニアのために実務でいるところだけ解説
WebGLにおいてGLSLを書く時、どうしても数学がでてきます。
ここでは数学(三角関数、ベクトル)を文系エンジニアのために、まず最初に抑えておきたいポイントだけ解説します。
難しいことは私もわかりませんし、GLSLを扱う上で、実案件ではほとんど必要ないです。(プログラムがやってくれます。本当にわかるともっと複雑なことができると思います。)
ただ、GLSLを書くときに知っておかないと理解しようがないポイントがあるので、
そのポイントのみを共有します。
定義の方法は、GLSLで定数を定義する方法(define, constとその違いと注意点)を参考にしてみてください。
三角関数
サイン・コサイン・タンジェントという言葉を聞いた覚えがあると思います。
それが、三角関数です。三角形に関する関数くらいの認識でいいです。
WebGLでは三角形を最小単位にしていろいろな形をつくるので、この三角関数が割とできてきます。
これの計算などはプログラムでできるので知る必要はないです!
大事なポイントは、このsin・cos・tan(サイン・コサイン・タンジェント)の値で曲線を作ることができるという点です。
「サインカーブ(正弦曲線)」、「コサインカーブ(余弦曲線)」、「タンジェントカーブ(正接曲線)」というのですが、
GLSL Grapherにてそれぞれのカーブを確認することができます。
まずは、サインカーブだけみてこんな感じかと知っておくといいでしょう。
x軸を中心に-1から1の間で波状になっているのが特徴です。
これを使うと、-1から1の間で値を動かせるので、図形を大きくしたり、小さくしたりをコントロールしたりすることが想像できると思います。
実際にそのように三角関数を使ったりします。
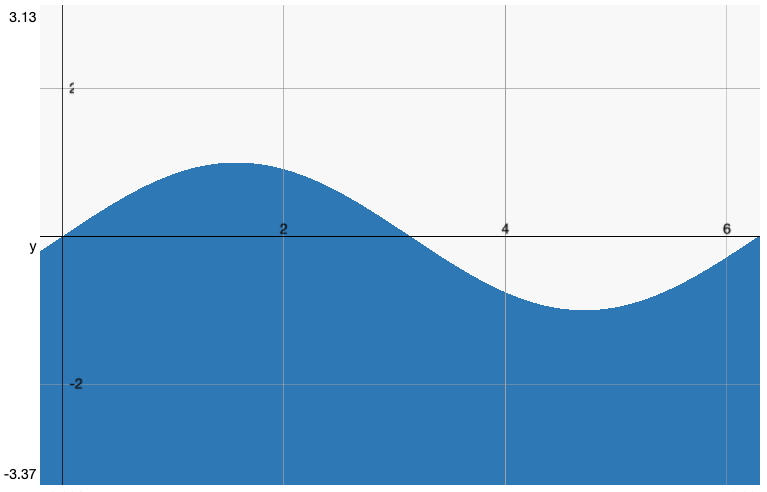
sin(3.14 * 2.0)また、上のようにしてPI(3.14)を2倍するとカーブの一周を意味します。
上で紹介したGLSL Grapherでみるとわかりますが、0を意味します。
sin(3.14 / 2.0)このようにすると、PIの1/2になるので、カーブの半分の半分、つまり1くらいになります。
これもGLSL Grapherで視覚的に確認してみるといいです。
ベクトル
ベクトルは矢印→です。これも高校あたりで習うのですが、社会人が長ければ長いほど記憶にないはずです。
実際にベクトルも可視化されたものを確認するのがいいので、以下サイトでいろいろいじってみることをおすすめします。
3Dベクトルの可視化サイトにてベクトルのイメージを掴めるとともに、
足したり、引いたり、かけたりすることができます。
足し引きは単純な算数で1+1=2みたいなものですが、掛け算だけは平面にたいして元のベクトルたちと90度別の方向に向かうベクトルになる、ということだけ知っておくといいです。
ベクトルの掛け算についてより深く知りたい人は、ベクトルの外積の求め方などで調べるといいです。
それでは実際にGLSLで計算してみましょう。
GLSLでのベクトル計算
まず定義から。
4次元ならvec4、
3次元ならvec3、
2次元ならvec2、
ベクトルでない値(スカラ値)ならfloat
を使います。
ベクトルの足し算
void main() {
// 足し算
vec4 v1 = vec4(0.0, 1.0, 0.0, 0.0);
vec4 v2 = vec4(0.0, 0.0, 0.0, 1.0);
vec4 color = v1 + v2;
gl_FragColor = color;
}fragment.glslで色を定義します。
この場合、RGBaのGだけが(0,1,0,1)とGreen(緑)だけが1になるので、緑色となります。
ベクトルの引き算
void main() {
// 引き算
vec4 v1 = vec4(1.0, 1.0, 1.0, 1.0);
vec4 v2 = vec4(0.0, 1.0, 1.0, 0.0);
vec4 color = v1 – v2;
gl_FragColor = color;
}
fragment.glslで色を定義します。
この場合、RGBaのGだけが(1,0,0,1)とRed(赤)だけが1になるので、赤色となります。
GLSL特有の計算方法
数値をまとめる
void main() {
// 引き算
vec4 v1 = vec4(0.5);
vec4 v2 = vec4(0.0, 1.0, 1.0, 0.0);
vec4 color = v1 - v2;
gl_FragColor = color;
}上のv1のように、vec4などの多次元で、一つの値だけを指定すると、すべての値をその値で指定することになります。
つまり、
vec4 v1 = vec4(0.5, 0.5, 0.5, 0.5);ということです。
代入する
void main() {
// 足し算
vec2 v3 = vec2(1.0); // vec2(1.0, 1.0);という意味
vec4 v1 = vec4(0.0, v3, 0.0);
vec4 v2 = vec4(0.0, 0.0, 0.0, 1.0);
vec4 color = v1 + v2;
gl_FragColor = color;
}上のようにすると、v3がv1の二番目に代入されます。
RGBaでいうと(0,1,1,1)になるので、水色になります。
スカラ値と計算する
void main() {
// 足し算
float f1 = 1.0; // スカラ値
vec2 v3 = vec2(0.0) + f1; //(1.0, 1.0)になる
vec4 v1 = vec4(0.0, v3, 0.0);
vec4 v2 = vec4(0.0, 0.0, 0.0, 1.0);
vec4 color = v1 + v2;
gl_FragColor = color;
}スカラ値はベクトルでない値です。
上の場合、floatがスカラ値で、vec2に足すと、二次元なのでそれぞれにスカラ値が足されます。
結果は上と同じになるためRGBaでいうと(0,1,1,1)になるので、水色になります。
識別子を使って値を指定する
// 座標: {x, y, z, w}
// 色: {r, g, b, a}
// テクスチャ座標: {s, t, p, q}上のような識別子があります。x,r,sなどどれでも同じ場所を示す識別子なのですが、
xyzwは、座標に使われることが多く、rgbaは色、テクスチャ座標は、stpqもしくはxyzwが使われることが多いです。
実際の使い方をみてみましょう。
void main() {
vec4 v1 = vec4(0.0, 1.0, 1.0, 0.0);
vec4 v2 = vec4(v1.gb, 0.0, 1.0);
vec4 color = v2;
gl_FragColor = color;
}上のようにして識別子をつかいます。
v1.gbというところは、v1のrgbaのg(1.0)とb(1.0)の2次元使っています。
つまり、v2は(1.0, 1.0, 0.0, 1.0)となるため、黄色になります。
この識別子は、v1.rrrなどもできて、3つ続けた場合は3次元になり、(0.0, 0.0, 0.0)を意味します。
v1.brgなど順番を入れ替えても使えますし、rgbaではなくxyzwにして、v1.zxyとしてもv1.brgと同じ意味になります。